Brachistochrone Curve|最速降下曲線

最速降下曲線(brachistochrone curve)は、1696年6月にスイスの数学者で物理学者の**ヨハン・ベルヌーイ(Johann Bernoulli)**が提唱したのが始まりです。
ベルヌーイは、当時の数学者たちに対して次のような問題を提示しました。
「2点間を最短の時間で降りる曲線を求めよ」
これが有名な「ブラキストクロノ問題(Brachistochrone problem)」です。
この問題に対しては、ヨハン・ベルヌーイ自身の他に、
- ヤコブ・ベルヌーイ(Johannの兄)
- アイザック・ニュートン(Isaac Newton)
- ゴットフリート・ライプニッツ(Gottfried Leibniz)
- ギヨーム・ド・ロピタル(Guillaume de l’Hôpital)
らが解答を寄せましたが、中でもニュートンは問題を受け取った翌日にすぐ解答を提示したと言われています。
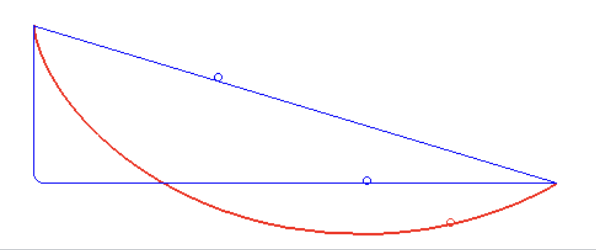
・目標を定めたときに、「最短距離」に見えるルートは実は最速距離ではない
・目標を定めたときに、最も短い時間で辿り着くための「最速ルート」は実はサイクロイド曲線である
結果として、最速降下曲線は数学的には「サイクロイド曲線(cycloid)」であることが判明しました。この問題は後に、変分法(calculus of variations)の発展につながる重要な契機となりました。
「Brachisto」の語源は、古代ギリシャ語の βράχιστος (brákhistos) に由来しています。この単語は、形容詞 βραχύς (brakhús)(意味:「短い」)の最上級形であり、文字通り、
- βραχύς(brakhús)= 短い
- βράχιστος(brákhistos)= 最も短い
という意味を持っています。
一方、「chrone」は、同じくギリシャ語の χρόνος (chrónos) に由来し、
- χρόνος(chrónos)= 時間
を意味します。
つまり、brachistochrone(ブラキストクロノ) は、
- brachisto (brákhistos) = 最短の
- chrone (chrónos) = 時間
を組み合わせたもので、「最短時間(で降下する)曲線」=最速降下曲線という意味になっています。
つまり、AからBに進むときに、直線距離で最短に見えるルートは、実は最速ではないということ。
一方でさらに、付け加えると、最速ルート≠最小作用である。Brachistochrone Curveは最小作用の原則の一部ではあるが、全体を示しているとは言えない。
AからBに進むときに、最速ルートは最小作用(時間✖️エネルギー)とは限らない。
・最小作用の原則(Least Action Principle)はエネルギーと時間の最適化問題である
・つまり、最小作用の原則はエネルギー✖️時間を最小化する
→最速であるルートが、最も効率的であるとは言えないということである。
→最速ルートは短期的な時間最小化を目指すが、最小作用ルート(LAP)は長期的な効率の収束(エネルギーと時間の最適なトレードオフの選択)を目指す。

